Air
2020年12月19日

图（Graph）

图（Graph）是计算机世界里常用的数据结构，它类似于一张地图，地图上有不同区域（Vertex），每一个区域是由高速公路（Edge）连接起来的。你常常会遇到图的应用场景，比如你在使用网约车的时候，会用到地图、你在社交网络上面的好友也是呈现网状结构、互联网本质上就是一张巨大的网。为了解决这些问题，我们需要在计算机里抽象出一种通用的数据结构-图（Graph），并定义图的相关操作和表示。接下来，我们将通过以下几个方面来学习图！

应用
定义
实现和操作
空间复杂度和时间复杂度

应用

现实世界里的许多问题均是由图数据结构来解决的，它们有:

互联网

互联网是一张巨大的网络，它上面连接了成千上万的节点，每一个节点代表着一张网页，网页与网页之间的连接是通过URL来建立的。市面上常用的搜索引擎就是基于图来建立，它能够抓取互联网上的网页，记录下每张网页上的URL，并基于这些信息来建立图。

社交网络

社交网络也用到了图数据结构，比如在Facebook里，你的一个朋友、一个会议、一张照片等等均可以抽象为图上的节点。当你发表一个状态时，和你连接的朋友均可以看到你的更新。同理，当你的朋友更新他们的状态时，你也能看到。这里用到了图数据结构以及相关的理论。

知识图谱

知识图谱也用到了图数据结构。简单来说，知识图谱将所有相关的知识连接在一起，比如关于文艺复兴时期的知识，可以延伸到但丁、莎士比亚、达芬奇等等。这些知识点均是图上的某个节点，并连接在一起，最终形成了一个知识图。常见的现实案例是Google的知识图谱，你在使用Google搜索引擎时，会看到从知识图谱中释放出来的信息。

路径优化

路径优化的问题也是我们经常会遇到的。比如，我们打开地图，想找到一条从北京到上海最短的路径，那么我们需要构建一个图，并为每条边附上距离。然后，在这个基础之上使用迪杰斯特拉(Dijkstra)算法求解出某个点到图上剩余点的最短路径。

科学计算

在科学计算领域，会经常设计一些算子，每个算子的输出结果是另外其它算子的输入结果，这些算子最后会通过连接形成一个图。除了算子，这个图上还会有其它类型的节点，比如输入参数或者预定好的参数。下图是一个用于Deep Learning的Flow Graphs，是一种有向图。

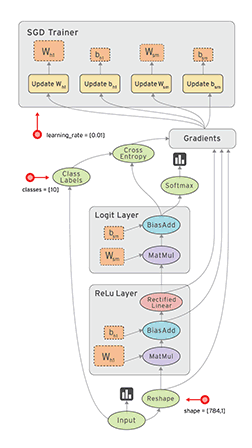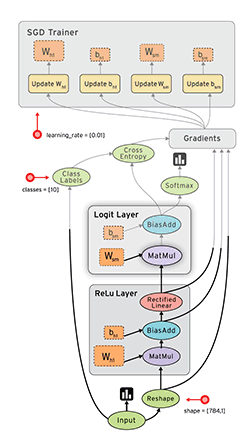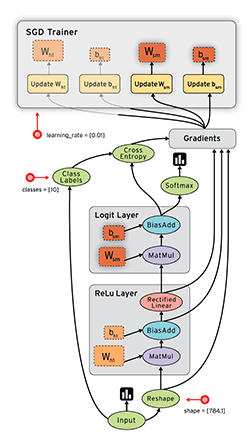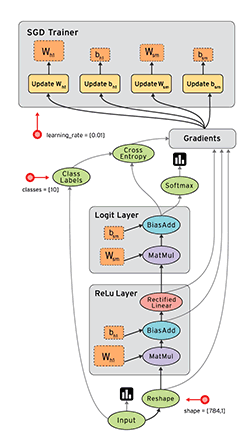
定义

首先来看看Wiki上的定义

In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from the field of graph theory within mathematics.

A graph data structure consists of a finite (and possibly mutable) set of vertices (also called nodes or points), together with a set of unordered pairs of these vertices for an undirected graph or a set of ordered pairs for a directed graph. These pairs are known as edges (also called links or lines), and for a directed graph are also known as arrows. The vertices may be part of the graph structure, or may be external entities represented by integer indices or references.

A graph data structure may also associate to each edge some edge value, such as a symbolic label or a numeric attribute (cost, capacity, length, etc.).

以上定义可以知道以下几点：

数学上有一个分支是专门研究图的，我记得上大学的时候专门还学过一门关于图的课程《图论》
在计算机科学中，图是一种抽象的数据类型，专门用于表示数学中的有向图和无向图
图类型由有限的顶点集（Vertexs）和边集（Edges）组成
每一个顶点一般都会记录一个索引，通过这个索引可以找到该顶点所对应的更加详细的内容
图上的每条边很有可能会记录一个数值或标签，比如从A顶点到B顶点的距离，就可以记录在AB这条边上

以下是一个关于无向图的示意图：

你可以把上面的示意图中每个顶点的数字理解为该节点的索引，通过这个索引，你可以查找到关于该节点更加详细的内容，而这些节点很有可能存储在某一个数组里。

在实现图的过程中，你需要处理以下几个问题：

通过什么方式来表示一个图。常见的方式有Adjacent list、Adjacent matrix以及Incidence matrix
如何遍历图上的所有节点。常见的遍历方式有深度优先遍历（DFS）和广度优先遍历（BFS）
提供关于图的操作。这些操作有添加一个顶点、删除一个顶点、添加一条边、删除一条边、获取与某个顶点相邻的其它顶点、判断2个顶点是否有边相连等等。

首先，让我们看看如何表示一个图，我们将对比2种方法：Adjacent list和Adjacent matrix，每种方法均有优缺点，你需要结合现实问题来选择。

Adjacent list的示意图如下所示：

这种表示方式由2部分组成，左边代表顶点集合，每一个顶点会关联与它连接的其它顶点，也就是上图右半部分。因此，当你准备用这种方式来表示图时，你需要创建一个顶点集合，并为每个顶点创建边集。

用这种方式表示图，有以下好处:

它的空间复杂度是O(V + E)。如果图的边不多，那么用这种方式来表示图会节约大量的存储空间
你可以通过顶点来直接获取它相邻的顶点
添加新顶点比较容易
添加新的边比较容易

当然，这种方式也会带来以下问题:

删除一个顶点的时候，需要遍历其它顶点的边
删除一条边的时候，需要遍历边上2个顶点所关联的边
判断2个顶点是否有边相连时，你需要遍历边上某个点所关联的边

如果你对图的操作经常会涉及添加点或边，那么可以考虑使用这种方式，但是，如果你对图的操作经常会涉及到删除边或者判断2个点是否相邻，那么你需要考虑另外一种图的表达方式Adjacent matrix。

Adjacent matrix的示意图如下所示:

这种方式是通过一个二维数组或矩阵来表示一张图。顶点通过数组的下标来标识，比如上图的顶点0和顶点1之间是是有边相邻的，因此(0，1)处的元素值是1，而顶点0与顶点2是没有边相连的因此(0，2)处的元素值是0。

用这种方式来表示图，有以下好处:

很容易就能通过顶点来判断两个顶点是否有边相连
为图增加或删除一条边也比较容易

当然，这种图也会带来以下问题:

增加一个顶点会比较麻烦
查找与某个顶点相连的顶点会涉及遍历
存储一张图的空间复杂度是O(V^2)，但是如果图的顶点数量远远大于边的数量，那么可以考虑使用稀疏矩阵解决这一问题

因此，如果你在使用图时，它的顶点数是固定的，而且顶点数远远大于边，频繁删除或增加边，频繁判断两个顶点是否有边相连，那么你可以考虑使用这种方式。

接下来，让我们处理图的另外一个问题:遍历。对于图的遍历，主要有2种方法:深度优先搜索(DFS)和广度优先搜索(BFS)。前者会借助栈数据结构来实现，而后者则用到队列来实现。接下来，让我们看看它们的区别。

DFS的思想是从某个顶点开始访问，把该顶点压入一个栈上，并将该顶点记录为已访问，接着获取某个与该顶点相连的且未被访问过的顶点，如果获取到未被访问过的顶点，那么将未访问的顶点压入栈，否则将当前栈顶的顶点弹出。重复整个过程，直到栈里不包含任何顶点，整个遍历就会结束。

BFS的思想是从某个顶点开始访问，并把该顶点排到队列里，并将该顶点设置为已访问。接着，把头部顶点从队列里取出，并把与该顶点相邻的且未被访问过的顶点压入队列。重复整个过程，直到队列中不包含任何顶点，到此，图的遍历就会结束。

最后，让我们看看常见的图操作：

增加或删除一个顶点：add_vertex(G, x)和remove_vertex(G, x)
增加或删除一条边：add_edge(G, x, y)和remove_edge(G, x, y)
判断2个顶点是否有边相连：adjacent(G, x, y)
获取某个顶点的value：get_vertex_value(G, x)和set_vertex_value(G, x, v)
获取某个顶点所关联的顶点：neighbors(G, x)

接下来，我们将选择Adjacent list方式来实现一个无向图。

实现和操作

在前面一节中介绍到，图可以通过Adjacent list来表示，这种表示方式需要考虑2点：顶点集和每个顶点关联的边集。

顶点集可以有多种选择，你可以选择数组，也可以选择链表，在这里，我选择Python中的dict，它是字典类型，该类型的基础数据结构是哈希表。至于每个顶点所关联的边集，我选择单向链表来表示。

整个图的Python版实现如下所示：

import singly_linked_list
import queue

class Vertex:
    def __init__(self, value):
        self.value = value
        self.associated_edges = singly_linked_list.SinglyLinkedList()

class Graph:
    def __init__(self):
        self.vertexes = {}

    def add_vertex(self, node_no, value):
        if node_no not in self.vertexes:
            node = Vertex(value)
            self.vertexes[node_no] = node

    def remove_vertex(self, node_no):
        if node_no in self.vertexes:
            associated_edges = self.vertexes[node_no].associated_edges
            removed_edge = associated_edges.remove_from_head()
            while removed_edge is not None:
                self.vertexes[removed_edge.key].associated_edges.remove(node_no)
                removed_edge = associated_edges.remove_from_head()

    def add_edge(self, node_no_1, node_no_2, cost):
        if node_no_1 in self.vertexes:
            self.vertexes[node_no_1].associated_edges.add_to_tail(node_no_2, cost)

    def remove_edge(self, node_no_1, node_no_2):
        if node_no_1 in self.vertexes and node_no_2 in self.vertexes:
            self.vertexes[node_no_1].associated_edges.remove(node_no_2)
            self.vertexes[node_no_2].associated_edges.remove(node_no_1)

    def neighbors(self, node_no):
        if node_no in self.vertexes:
            return self.vertexes[node_no].associated_edges

    def set_vertex_value(self, node_no, value):
        if node_no in self.vertexes:
            self.vertexes[node_no].value = value

    def get_vertex_value(self, node_no):
        if node_no in self.vertexes:
            return self.vertexes[node_no].value
        return None

    def adjacent(self, node_no_1, node_no_2):
        if node_no_1 in self.vertexes and node_no_2 in self.vertexes:
            return self.vertexes[node_no_1].associated_edges.find(node_no_2) is not None
        return False

    def dfs(self, start_node_no, call_back):
        if start_node_no in self.vertexes:
            visited = {}
            stack = []
            stack.append(start_node_no)
            while len(stack) != 0:
                top = stack[0]
                if visited[top] is None:
                    call_back(self.vertexes[top].value)
                    visited[top] = True
                # get unvisited node
                associated_edges = self.vertexes[top].associated_edges
                current_node = associated_edges.head
                while current_node:
                    if visited[current_node.key] is None:
                        break
                    current_node = current_node.next
                if current_node is not None:
                    stack = [current_node.key] + stack
                else:
                    stack = stack[1:]

    def bfs(self, start_node_no, call_back):
        if start_node_no in self.vertexes:
            visited = {}
            dequeue = queue.DeQueue()
            dequeue.push_back(start_node_no)
            while not dequeue.empty():
                front_node = dequeue.pop_front()
                visited[front_node] = True
                call_back(self.vertexes[front_node].value)
                associated_edges = self.vertexes[front_node].associated_edges
                current_node = associated_edges.head
                while current_node:
                    if current_node.key not in visited:
                        dequeue.push_back(current_node.key)
                    current_node = current_node.next

你也可以运行以下指令来clone完整源码：

git clone https://github.com/digolds/data-structure-algorithm.git

以上就是一个基于Adjacent list的无向图，接下来，让我们看一看这些方法的空间复杂度和时间复杂度。

空间复杂度和时间复杂度

分析图的复杂度，你需要从以下几个操作入手：

表示一张图的空间复杂度是O(V+E)
添加一个节点的时间复杂度是O(1)，空间复杂度是O(1)
删除一个节点的时间复杂度是O(e)，e是删除节点所关联的边，空间复杂度是O(1)
添加一条边的时间复杂度是O(1)，空间复杂度是O(1)
删除一条边的时间复杂度是O(e)，e是删除节点所关联的边，空间复杂度是O(1)
获取某个顶点的关联边的时间复杂度是O(1)，空间复杂度是O(1)
DFS的空间复杂度是O(V)，时间复杂度是O(V+E)
BFS的空间复杂度是O(V)，时间复杂度是O(V+E)

{{ c.user.name }}
- {{ c.display_datetime }}
{{ c.content }}

请登录购买（{{ selected_gold.price }}元），即可解锁剩余教程

点击购买

{{ s.title }}
{{ a.title }}
{{ a.title }}

{{ title }}

图（Graph）

应用

互联网

社交网络

知识图谱

推荐引擎

路径优化

科学计算

定义

实现和操作

空间复杂度和时间复杂度

{{ c.user.name }}

{{ title }}

{{ selected_gold.title }}

{{ title }}

图（Graph）

应用

互联网

社交网络

知识图谱

推荐引擎

路径优化

科学计算

定义

实现和操作

空间复杂度和时间复杂度

创建新文章

删除文章或章节

{{ title }}